Biography
My long standing research interests relate to the role of strain and elastic relaxations in minerals and functional materials. These play a fundamental role in determining the nature, mechanisms and thermodynamic character of phase transitions and in controlling the properties of solid solutions. The fundamental principles apply across the solid state sciences, from Earth Sciences to Materials Physics and Engineering.
I welcome opportunities to develop collaborative ventures in aspects of strain and elasticity that arise in Earth Sciences, Solid State Chemistry, Solid State Physics, Materials Science, Engineering or Biomaterials. Anyone who would like to make elasticity measurements in my Resonant Ultrasound Spectroscopy lab should feel free to contact me at any time. I also welcome enquiries from potential students and post-docs.
Materials of current interest (all in collaborative ventures) include: minerals, relaxor ferroelectrics, ferroelectrics, ferro/antiferromagnetics, multiferroics, metallic glasses, metal-organic frameworks, martensites, Heusler compounds, Ti alloys, unconventional superconductors.
Current funding is for "Magnetoelastic coupling behaviour and multiferroicity of magnetic iron oxide and sulphide minerals" (Leverhulme Trust), and "Ferroelectric, ferroelastic and multiferroic domain walls: a new horizon in nanoscale functional materials" (EPSRC, with JM Gregg, M Alexe, JF Scott, EKH Salje)
Thanks to many collaborators – particularly, Ekhard Salje, Chris Howard, Jim Scott, Tim Darling, Albert Migliori, Richard Harrison, Ruth McKnight, Zhiying Zhang, Jason Schiemer, Don Evans, Wei Li, Oktay Aktas, Catalina Salazar, Sarah Driver and others.
LLLXXXXXXXXXXXXXXXXXXXXXXXXXXXLLLXXXXXXXXXXXXXXXXXXXXXXXXXXXXLLL
Thanks to funding agencies – particularly, NERC, EPSRC, The Leverhulme Trust
Research
Phase transitions, strain, elasticity and anelastic phenomena in minerals and functional materials
1. Phase transitions
Phase transitions are by definition collective phenomena. Some local instability in the atomic or electronic configuration of a structure develops correlations over a significant length scale, macroscopic symmetry is broken and a new long-range order is established. Changes in symmetry conform to group theoretical constraints, giving rise to the concept of order parameters and providing the rigorous underpinning of Landau theory.
2. Strain and elasticity
It is well understood that strain has a fundamental and pervasive influence on almost all types of phase transitions, either as the driving order parameter (acoustic mode instability) or by coupling with some other driving mechanism, which may be structural (soft mode, atomic ordering, hydrogen bonding….), ferroelectric (displacive, order/disorder, relaxor….), magnetic (ferro/antiferromagnetic, spin-glass….), or electronic (charge order, Jahn-Teller, spin state, superconducting, metal-insulator….).
The most overt implications are firstly that the correlation length of the order parameter takes on the generally longer length scale of strain fields, secondly that overlapping strains from otherwise separate order parameters can result in strong coupling between multiple instabilities and, thirdly, that transformation microstructures such as tweed and twin walls may interact strongly with defects. Some of the consequences relate to reduction of the Ginsburg temperature interval of critical fluctuations, an expectation that mean field models should provide effective descriptions of thermodynamic properties, a tendency for transitions which would otherwise be second order to become first order in character, interdependence of different physical properties such as ferroelectricity and magnetism, and control of the dynamics and mechanisms of switching by strain relaxation or defect pinning processes.
Understanding the behaviour of bulk samples also feeds into considerations for thin film technologies since a key variable is the coherency strain of the film with its substrate. The choice of substrate is a choice of imposed strain which, in turn, drives a strain coupled order parameter in the film to some desired configuration and magnitude. There will be subtle differences, however, since the imposed strain will be homogeneous, whereas a bulk material containing ferroelastic twin walls or polar nano regions, for example, will contain strain heterogeneities at a local, mesoscopic length scale.
In the context of multiferroic materials, direct magnetoelectric coupling tends to be weak, as represented by the small overlap of fields for ferro/antiferromagnetism and ferroelectricity, but if both the ferroelectric dipole and the magnetic order parameter each couple with a co-elastic or ferroelastic strain the (indirect) coupling may be substantially increased.
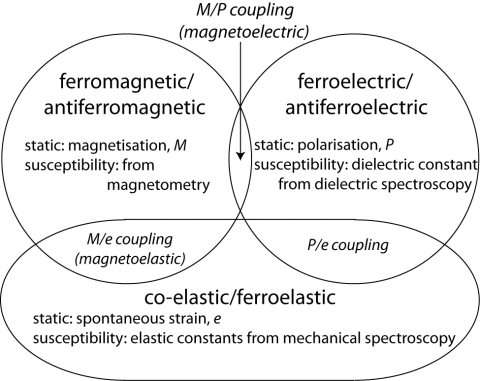
Any change in strain state of a material will give rise to an associated change in elastic properties. Because the elastic constants are susceptibilities they can vary by tens of % and thus provide highly sensitive indicators of the strength and style of any strain coupling which may occur, even when the magnitudes of the strains themselves are on the order of or less than 1%.
Order parameters and spontaneous strains depend on symmetry such that the form of coupling between them is also determined by symmetry, as can be developed effectively using Landau theory. A wide variety of patterns of evolution with temperature, pressure and applied field is possible and, in principle, should provide insights into the strength, mechanisms and dynamics of strain coupling for any particular material of interest.
2. Elasticity measurements by Resonant Ultrasound Spectroscopy (RUS)
Most methods of measuring elastic moduli are dynamic and the best analogy is with measurements of dielectric properties. The dynamically applied field is stress (electric field) and the response has real and imaginary components which are typically used to evaluate the elastic compliance (dielectric permittivity) and acoustic loss (dielectric loss) as functions of temperature and frequency. However, while the frequency of an electric field can be adjusted continuously through many orders of magnitude, there is no single experimental method for measuring elastic properties over a wide frequency interval. Instead, a number of different methods are used in relatively narrow frequency windows.
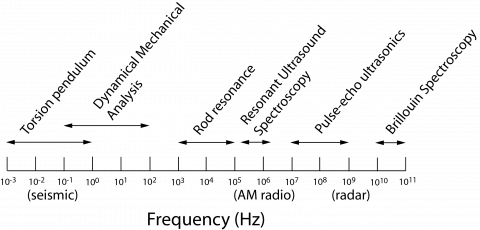
Resonant Ultrasound Spectroscopy (RUS) has provided a convenient method for investigating elastic and anelastic anomalies associated with phase transitions due to its simplicity in terms of sample size and mounting. In addition, it appears that the frequency range near 1 MHz, combined with small imposed stresses, provides a particularly sensitive window on microstructure dynamics.
|
|
Cambridge low temperature RUS head, showing a sample cut in the shape of a rectangular parallelepiped with dimensions ~3x4x5 mm3. The sample is held lightly across a pair of corners or a pair of faces between two piezoelectric transducers, one of which is used to scan in frequency between ~0.1 and ~3 MHz and the second to detect acoustic resonances which are excited at particular frequencies. Resonance peaks with frequency f in the spectrum are predominantly due to shearing modes and are constrained by individual elastic constants or combinations of elastic constants whose absolute values scale with f2. A direct measure of acoustic dissipation in the sample is given by the inverse mechanical quality factor, Q-1, which depends on the peak width at half height, Df, according to Q-1 = Df/f. For a polycrystalline sample, shear and bulk moduli are obtained by fitting the frequencies of ~10-20 peaks. Single crystal elastic constants can also be obtained. |
|
|
Cambridge high temperature RUS system. The sample is held lightly between the tips of alumina buffer rods which protrude into a horizontal resistance furnace. The driving and detector transducers are glued to the other ends of the buffer rods and remain outside the hot zone. A separate system with essentially the same design is encased so as to allow the sample to be held in a controlled atmosphere. |
|
|
Oxford Instruments Teslatron, with RUS head, allowing collection of RUS spectra in the temperature range 2-305 K with simultaneous magnetic field up to 14 T. |
3. Elastic anomalies associated with phase transitions
An illustration of the data obtained by automatic collection of RUS spectra through a sequence of phase transitions is provided for KMnF3. Individual spectra from an irregularly shaped single crystal, with mass 0.3354 g and approximate dimensions 10 x 10 x 1 mm3, are stacked in proportion to the temperature at which they were obtained. The sequence of transitions is Pmm (paramagnetic) – I4/mcm (paramagnetic) at ~185 K, I4/mcm (paramagnetic) – Cmcm (antiferromagnetic) at ~87 K, Cmcm (antiferromagnetic) – Pnma (canted antiferromagnetic) at ~83 K.
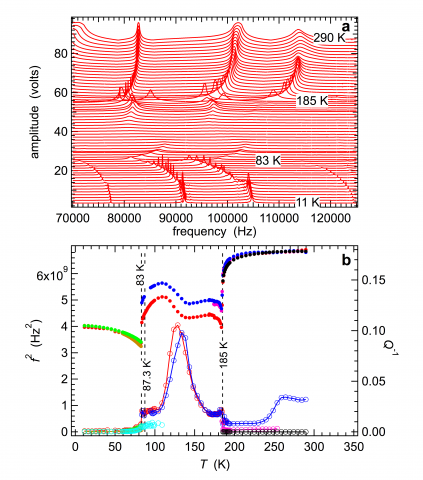
Substantial softening, evident as shifts to lower frequencies of individual resonance peaks, and an increase in loss in the stability field of the I4/mcm structure, evident as peak broadening, are confirmed in the variations of f2 and Q-1. Softening of the elastic constants by up to ~40% is due to the development of shear strains associated with the octahedral tilting transitions but there is no overt evidence of contributions from magnetoelastic relaxations. The Debye-like loss peak centred on ~130 K has been attributed to freezing of ferroelastic twin walls due to pinning by F vacancies or dumbbell pairs of F interstitials
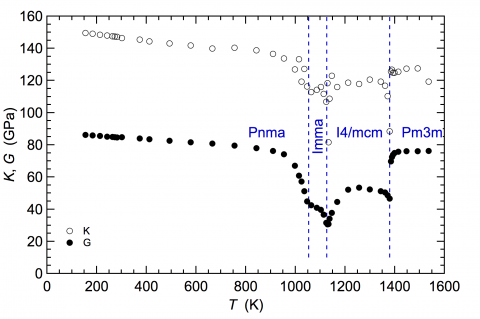
An example of quantitative results for the bulk, K, and shear, G, moduli is given below for a polycrystalline sample of SrZrO3 through the sequence of octahedral tilting transitions Pmm – I4/mcm – Imma – Pnma. Experimental uncertainties obtainable for samples of this type are ~0.1 % for G, and ~1% for K, though these become higher in the vicinity of transition points where the number of measurable resonance peaks reduces due to acoustic attenuation. The phase transitions are accompanied by characteristic patterns of elastic softening and stiffening, up to ~45%, due to coupling of shear and volume strains with the tilt order parameters.
4. Magnetoelastic coupling
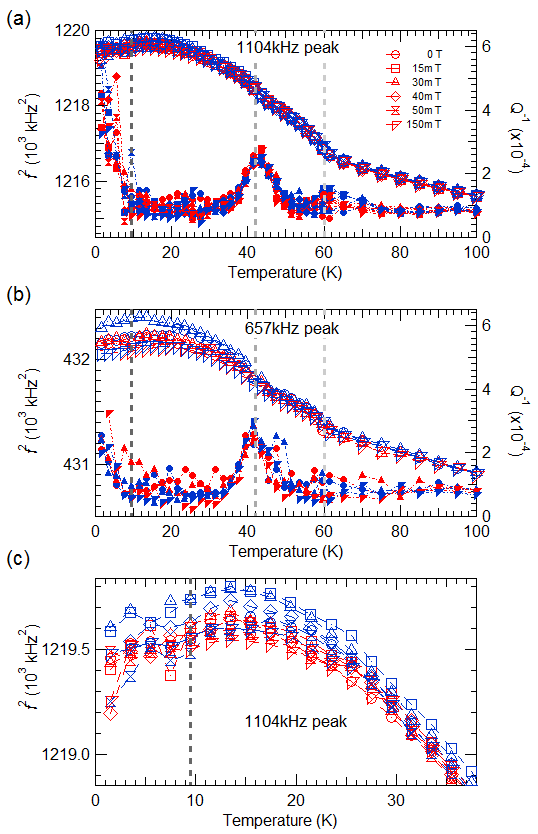
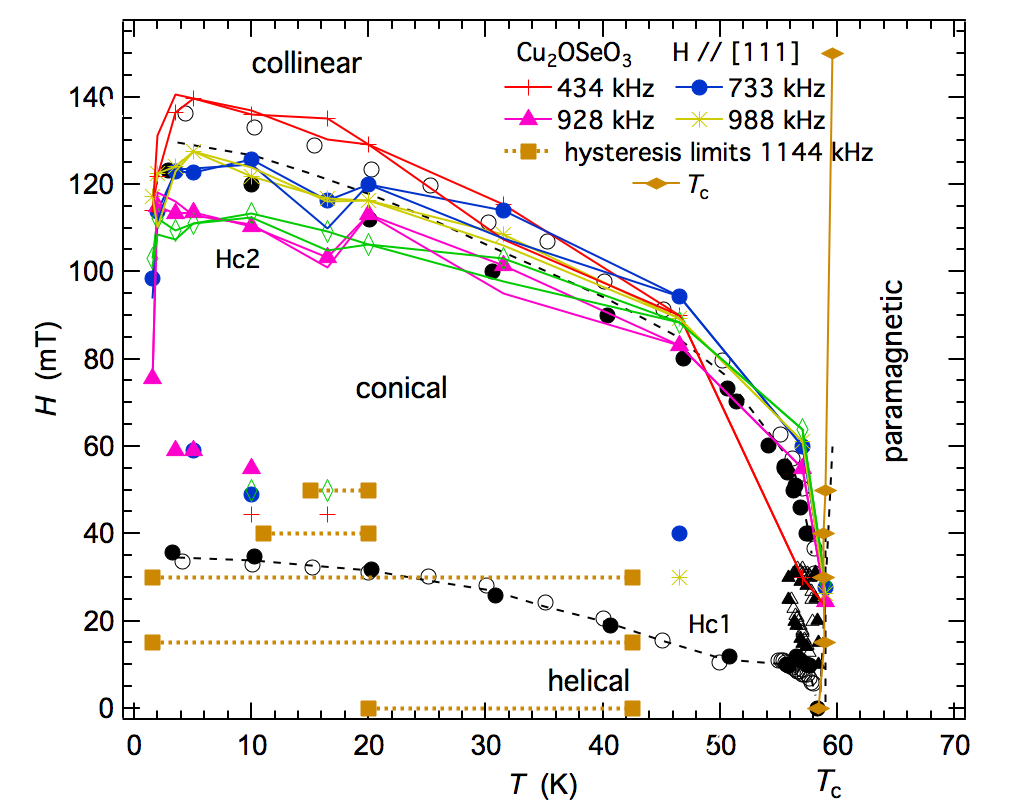
Magnetic transitions are typically accompanied by strains which are often referred to as spin-lattice coupling. The strength of such coupling is enormously variable. One example is provided by small but significant static and dynamic strain coupling effects in Cu2OSeO3 associated with magnetic phase transitions observed as a function of temperature (1.5-150 K) and magnetic field (0-300 mT). The magnetic transition near 60 K is accompanied by a small increase in single crystal elastic constants which can be understood in terms of biquadratic coupling between shear strain and the magnetic order parameter, even though the shear strain itself is negligibly small. The conical – collinear transition is associated with distinct minima in the elastic properties, while weaker anomalies at lower fields may be related to changes in the configuration of magnetic domains. A distinctive acoustic loss peak at ~42 K, independent of magnetic field, is attributed to freezing of a defect which is coupled with shear strain, has an associated activation energy of ~5 kJ.mole-1 and may play some role in pinning the magnetic microstructures. Anomalies below ~10 K indicate the presence of some additional relaxation process which could signify a change in magnetic structure. (Evans et al, 2017, Phys Rev B 95, 094426).
|
|
Variation in (resonance frequency)2, which scales with a combination of single crystal elastic constants, and Q-1, which scales with acoustic loss through the helical magnetic transition at 69 K. There is a small increase which follow the square of the order parameter. The peak in Q-1 at ~42 K indicates a freezing process which is probably pinning of the helical structure to defects. |
|
|
Location of anomalies in single crystal elastic constants of Cu2OSeO3 in relation to the known phase diagram for external magnetic field applied parallel to [111]. |
5. Anelasticity associated with phase transitions
Anelastic losses occur in crystals when the response to an externally applied dynamic stress involves some relaxation which is coupled to a strain and which has a relaxation time that is concomitant with the frequency of the applied stress. The strain may be coupled to an intrinsic process, such as proton ordering in lawsonite, CaAl2Si2O7(OH)2.H2O. Alternatively, the relaxation process could be extrinsic, such as displacements of impurity atoms or transformation microstructures.
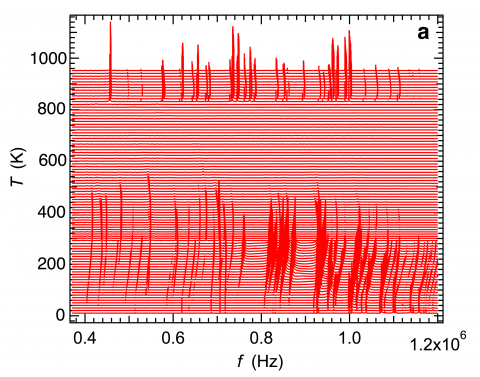
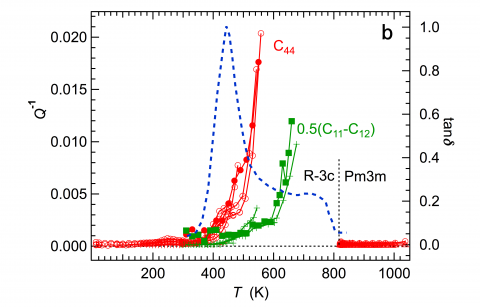
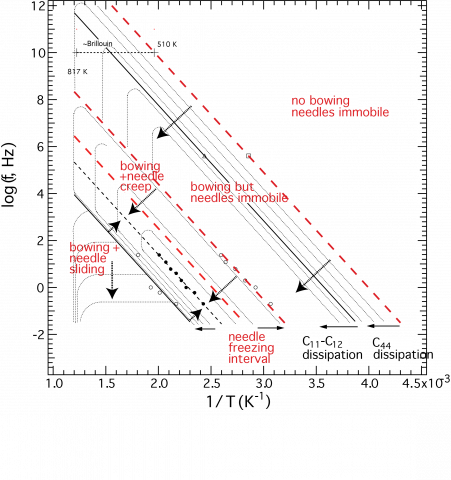
The influence of twin walls due to ferroelastic transitions is illustrated by the case of LaAlO3. The octahedral tilting transition is marked by an abrupt disappearance of resonance peaks from spectra collected below Tc (817 K) and is attributed to the motion under external stress of ferroelastic twin walls in the rhombohedral structure. This complete attenuation (“superattenuation”) implies maximum values of Q-1 greater than ~0.02 and continues until the resonance peaks gradually reappear below ~600 K when the mobile twin walls become pinned by interaction with defects.
|
|
Segments of RUS spectra obtained from a single crystal of LaAlO3 stacked in proportion to the temperature at which they were collected. Resonances disappear abruptly below Tc = 817 K (superattenuation) and reappear as broad peaks below ~600 K. |
|
|
|
Variation of Q-1 from RUS spectra (left axis, joined up data points), compared with the variation of tand from Dynamical Mechanical Analysis data (right axis, dashed curve). The pattern of loss is qualitatively similar but the freezing temperatures are not consistent with a single mechanism. It seems likely that the relatively high stress in DMA causes movement of the tips of needle domains while the relatively low stress conditions of RUS result in local displacements of twin walls by a ledge mechanism. |
|
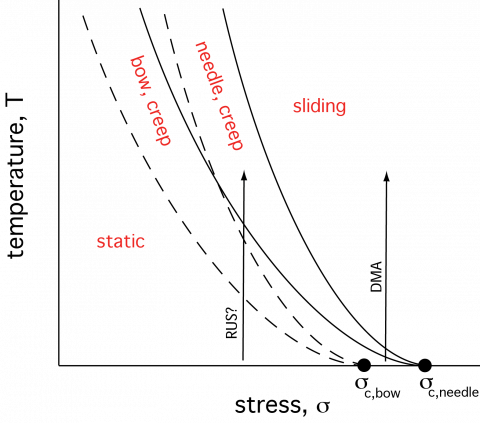
As with mechanisms of plastic deformation, there are regions of parameter space in which different mechanisms will operate and these can be represented in anelasticity maps of the form shown schematically for the mobility of ferroelastic twin walls in LaAlO3.
|
|
|
6. Resonant Piezoelectric Spectroscopy (RPS)
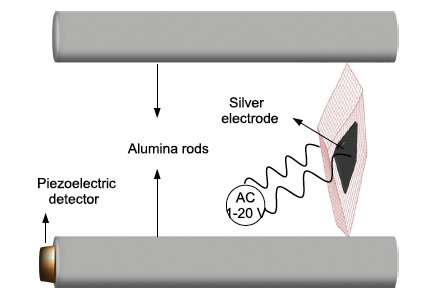
A new adaptation of the RUS method for characterising ferroic materials and their possible adaptive states is to stimulate resonances of the samples by an ac electric field instead of mechanically by a piezoelectric transducer (Resonant Piezoelectric Spectroscopy, RPS). A schematic view of the experimental configuration is given below. If the sample is intrinsically piezoelectric or if it contains locally polar regions, mechanical resonances can be excited by the ac electric field. These are detected by the transducer and their frequencies should be the same as obtained by mechanical excitation in a conventional set up for RUS. RPS allows the detection of polarity in domain walls and within tweed or other nanodomain microstructures with high sensitivity.
|
|
Schematic view of the experimental configuration for RPS (*Aktas et al 2013 Appl Phys Lett 103 142902). An alternating electric field is applied to silver electrodes on opposite sides of a sample which would typically be ~1x3x3 mm3. The configuration is shown for high temperatures, where the sample sits on alumina buffer rods inside a horizontal resistance furnace and the detector transducer is outside the furnace. |
Publications
Recent publications can be found in the publications database here
Please accept marketing cookies to show embedded content (open cookie preferences)